Imagine, says Pope, that you are a classical physicist like Galileo or Newton and that you think of space and time in the way they did. Space would be spread out everywhere all at the same time, in a universally extended present moment, and time would be a universal succession of those present moments in a kind of cosmical GMT. The space would be measured in units of pure distance such as, say, conventional metres, and the time would be measured in conventional units of seconds.
Next, Pope says, imagine that someone like Olaus Römer discovers that these units of space and of time are related in a constant ratio, c, of 300,000,000 metres to the second for all observers regardless of their states of motion or rest with respect to one another. Space and time, which were initially thought of as independent measures now become dependent measures. It would be as if the dimensions of length had been traditionally measured in metres and those of breadth in inches and then someone discovered that there are always 39.37 inches in a metre. The result, of course, would be that what you had thought of as the three rectangular dimensions of space and the geometrically unrelated dimension of time are now geometrically combined into a four-dimensional system of rectangular measures in which, if time is measured in seconds, then so are distances - or in units of 300,000,000 metres divided by c, which is the same thing.
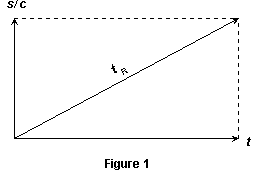
In this geometrical four-dimensional space-time the distance s in metres, travelled by a moving body becomes a distance-time s/c measured in seconds, as depicted in Figure 1. The measure of the body's motion is then that distance-time s/c travelled by the body in the time t of that motion as registered by the moving body itself (see figure).

Now the fact that those two rectangular components of the motion are measured in the same units of seconds gives to that motion-diagonal a geometrical significance expressed by the Pythagorean relation:
where tR is the observational or relativistic resultant of the two motion components s/c and t.
Plainly, then, without ever having heard of Einstein, it would have been possible for a classical thinker to have deduced what Einstein deduced regarding the relativity of time, simply by taking c as a dimensional constant instead of as Einstein's strange and unnecessary 'velocity relative to the vacuum'. However, if required, Einstein's more familiar, mathematically complicated and logically circuitous version of relativity can be obtained from the Pythagorean space-time formula by substituting for s in that formula the Einsteinian equivalent vtR and then simplifying, which produces the usual formula: